Теорія ігор і дизайн механізмів 2. Тістечко з горішками та інші історичні приклади.
- 5 років тому
- Наука
- 5 240
- 501
- 34
- 13
Нобелівська премія з економіки 2007 року була вручена Гурвічу, Маскіну та Майерсону за “розробку основ теорії дизайну механізмів”. Як уже зазначалось у попередній публікації, дизайн механізмів це, в певному розумінні, обернена інженерія економіки. Як побудувати правила, які будуть спонукати людей діяти так, як ми хочемо? Левова частка результатів цієї теорії відноситься до області теорії ігор, оскільки загалом люди ведуть себе раціонально - приймають рішення намагаючись покращити свій результат.
Тістечко з горішками
Згадаємо гру про поділ тістечка. Уявімо собі, що в тістечку є горішки, і ці горішки нерівномірно розподілені (цей приклад наводить у своїй книзі Роджер МакКейн ). І ми знаємо, що на правій стороні їх більше, тільки не питайте звідки ця інформація. Тістечко хочуть поділити двоє гравців, але тепер гравці різного типу. Перший (назвемо його А) любить горішки і, навіть, готовий вибрати менший шматок, якщо там їх більше. Другий гравець (тип Б) не має ніяких почуттів до горішків і просто хоче шматок побільше. Що таке “чесний поділ” в цьому випадку? Ми назвемо поділ беззаздрінсим, якщо кожен з гравців вважає, що він отримав кращий або такий же шматок (тут немає протиріччя, оскільки у них різне розуміння, що таке краще). Очевидно, він має залежати від уподобань гравців, які є їх таємною інформацією. Звичайно, гравці можуть прямо сказати про свої уподобання, але відразу виникає проблема - коли і кому можна вірити?
Адже світ бентежний, повний маніпуляцій і “всі брешуть”.
Розглянемо схему “Б ділить тістечко, А вибирає”. Якщо Б знає уподобання А, то він може розділити тістечко на два не рівні шматки, менший з великою кількістю горішків і більший з меншою. А вибере шматок з горішками і всі щасливі. Ця схема буде узгоджена з уподобаннями гравців.
Але тут виникає питання: а як Б може бути впевнений, що А той, за кого себе видає? Можливо А не хоче більше горішків, а просто намагається отримати більше тістечка? Звичайно, Б може спитати напряму, але як можна вірити будь-якій відповіді? Якщо А дійсно любить горішки, то він скаже, що любить горішки. Якщо А не любить горішки і просто хоче отримати більший шматок - він теж скаже, що любить горішки.
Оскільки А ходить другим, то як би він не переконував Б, ніяких гарантій він надати не може і може статись трагедія: Б розріже на два нерівних шматка і залишиться з меншим.
Ось тут і виникає проблема, яка призвела до появи теорії дизайну механізмів: Як створити механізм, який би давав гравцям можливість говорити правду? Виявляється, що це можливо і в результаті гравці, які говорять правду отримають не менше ніж ті, що брешуть (тобто немає стимулів брехати про свій тип).

Замість горішків можна уявляти тістечко з іншими асиметричними добавками. А хоче більше малини (але це не точно ), Б хоче більше тістечка.
Ігри Байеса-Неша
Для кращого розуміння суті проблеми потрібно описати ідею рівноваги Байеса-Неша та сигнальних ігор (розкажу про це на прикладі, без формул). Приклад спеціально вибраний “не серйозний”, але ситуація невизначеності та асиметрії інформації є ключовою в багатьох іграх. Згадайте, наприклад, Джорджа Акерлофа з його лимонами.
Отже ситуація наступна: по вулиці йде гопник, який хоче з кимось побитись. Він уже в такому стані, коли важко розрізняє деталі інших і може лише бачити, що вони тримають у руці (це сигнали, які він отримує). Йому відомо, що вулицею можуть гуляти гравці двох типів: роботяги і хіпстери. Вони можуть тримати в руці пляшку з пивом або стаканчик кави флет-вайт.
При цьому виграші гопника залежать від типу опонента. Бійка з хіпстером приносить йому задоволення 1, а бійка з роботягою не дуже цікава - виграш 0. Ні роботяги ні хіпстери не зацікавлені в бійці і вони можуть вплинути на це вибираючи сигнал - пити пиво чи каву флет-вайт.
Якщо гравець п’є свій улюлений напій і з ним ніхто не б’ється, він отримує 3. Якщо напій улюблений але все таки бійка, то він отримує 1.
2 він отримує у ситуації, коли він вибрав інший (не улюблений) напій і бійки немає, тобто обманув гопника і це спрацювало, і 0, якщо зміна не спрацювала.
Дерева гри для випадку повної інформованості зображені нижче.
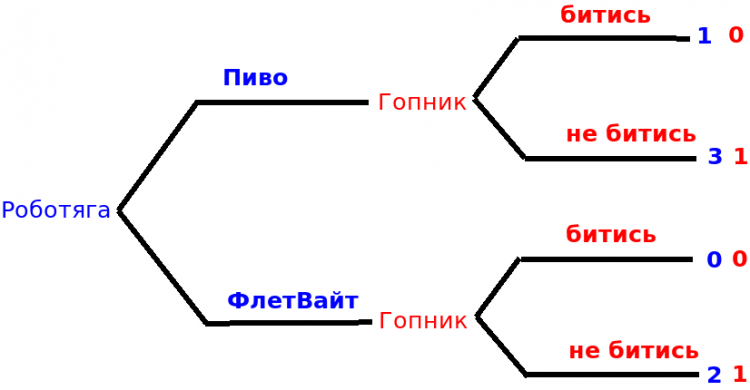
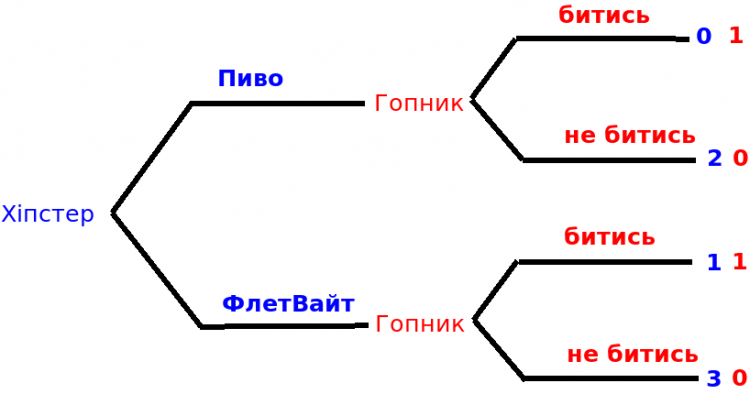
Якщо гопник знає тип гравця перед ним, то його стратегія проста - завжди бити хіпстера і не лізти до роботяги - це дає йому найбільший виграш.
Але що буде, якщо гопник не знає справжній тип, а бачить тільки сигнал від нього? Оскільки гопник не знає тип, потрібно використовувати умовні ймовірності, тому ці ігри отримали назву ігри Байеса-Неша. Не заглиблюючись у деталі, припустимо, що роботяг вдвічі менше ніж хіпстерів, тобто ймовірність зустріти хіпстера ⅔ , а роботягу ⅓ .
Тоді у гопника виникає проблема вибору стратегії: якщо він бачить типа з кавою, то, можливо, це роботяга, який взяв каву замість пива? А коли він бачить типа з пивом, то, можливо, це хіпстер, що маскується?
Аналогічне питання виникає у інших гравців: що робити? Взяти пиво замість улюбленого флет-вайту і це врятує від бійки, чи бійка буде в будь-якому разі і тоді пиво не рятує (і нащо його тоді брати)?
Виявляється, що для описаної вище задачі раціональний розв’язок існує (він дається рівновагою Байеса-Неша). Наведемо лише фінальну відповідь:
- Стратегія роботяги: завжди пити пиво.
- Стратегія хіпстера: пити пиво в половині випадків, пити каву в половині випадків.
- Стратегія гопника: якщо в руці кава флет-вайт битись завжди, якщо в руці пиво битись з ймовірністю 0.5.
В стані рівноваги кожен хіпстер має шанс уникнути бійки обираючи пиво. Якщо він обере каву, то бійка буде з ймовірністю 1, але з пивом він має 50% шанс уникнути її. Пиття пива є сигналом гопнику, що з ним не треба битись. Цей сигнал має вартість (особа має змусити себе пити пиво замість смачного флет-вайту) і саме тому він працює. До речі, є цілий напрямок теорії ігор як подавати сигнали, які дійсно працюють.
Оскільки роботяги завжди п’ють пиво, то гопник не може бути 100% впевненим, хто перед ним, тому він змушений іноді відмовлятись від бійки, але не завжди. Якщо гопник буде завжди відмовлятись від бійки, отримавши сигнал “я з пивом”, то він вже ніколи не знайде хіпстерів з кавою.
Ігри Байеса-Неша досліджують подібні ситуації, а механізм дизайн пробує запропонувати схему, яка б “просвічувала” гравців та змушувала їх розкрити свій тип.
Ідея більш економічної версії дизайну автоматично призначає виграш відповідно до типу і цей виграш є рівноважним (тобто хорошим). Тоді б гравцям не потрібно було б приховувати свій тип.
Проблема визначення типу за допомогою “механізму” не нова, її часто використовували різні політики, інтригани та талановиті маніпулятори. Ось декілька цікавих історичних прикладів.
Жао Гао
Хрестоматійна китайська історія про могутнього євнуха Жао Гао, який поступово перетворив імператора на маріонетку. Одного разу Гао вирішив посилити свою владу, знищивши можливих опонентів. Але як дізнатись хто підтримує його насправді, а хто лише робить вигляд? Тоді він приніс у подарунок імператору оленя і сказав “Я дарую Вам коня”. Імператор, невпевнена і безвольна людина все таки повірив очам і сказав - “Так це ж олень”. Але євнух хитро запропонував спитати у інших придворних. Коли імператор спитав, деякі промовчали, деякі підтвердили, що це кінь, деякі сказали, що це олень. Пізніше Гао знищив всіх, хто сказав правду, підвищив всіх хто збрехав і в результаті отримав всю владу.

Гао придумав механізм виявлення нелояльних йому людей.
Стріла, що свистить
Інший, не менш цікавий приклад. Отже, територія Монголії, кочівники хунну пару тисяч років назад. Старший син хана виявився незручним після того, як хан одружився вдруге на дівчині з важливого клану. Декілька замахів, потім підстава під час бою, полон. Під час переговорів про викуп послів страчують, прозоро натякаючи, що слід зробити з бранцем. Але сталось так, що принц тікає з під варти, самотужки долає пів великого степу і повертається героєм. Батько змушений прийняти неочікуваного спадкоємця та навіть надати особисту охорону з 1000 відбірних воїнів. Звичайно принц розумів, що ці почесті тимчасові і нічний вбивця або отруєне вино закінчать справу.
І тоді він почав готувати свою гру. Потрібний йому механізм повинен був відділити тих воїнів, хто був готовий слідувати йому без роздумів від тих, хто був не зовсім лояльним або і засланим шпигуном.
Принц підготував три стріли, які свистять у повітрі і наказав своїм воїнам не роздумуючи стріляти у тому напрямку куди він випустить свою стрілу. Першу стрілу принц випустив у свого улюбленого скакуна. Ті хто не вистрілив були страчені. Другу стрілу принц випустив у свою молоду красуню дружину. Ті хто не вистрілив були страчені. Нарешті третя стріла під час ловів полетіла у старого хана. На цей раз всі стріли полетіли в ціль, а принц став новим ханом.
Паркінсон: як вибрати Президента
Книга Сирила Паркінсон “Закони Паркінсона” містить високу концентрацію британського гумору, але також є чудовим дослідженням прийняття рішень в ситуаціях бюрократії, суспільства і т.н. Один з розділів присвячено проблемі вибору людини на посаду. Описані класичні успішні методи (старий китайський, новий китайський, старий британський і новий британський) і чому вони не зовсім працюють. Але потім Паркінсон пропонує свій метод, який, по суті, є механізмом в сенсі теорії ігор. Я спробую викласти його ідею тут з поправками на наші реалії.
(далі буде дуже вільний переклад, навіть варіації на тему, сама книга українською не перекладалась)
Отже, припустимо нам потрібен президент для якоїсь проблемної східноєвропейської країни. По-перше, потрібно визначити, які якості мають бути присутні. Припустимо, що це:
- Енергія
- Сміливість
- Патріотизм
- Досвід
- Популярність
- Вміння виступати
Однак, будь-який кандидат в президенти знайде ці навички у себе. Звичайно, можна ускладнити вимоги, наприклад 4. досвід у приборканні левів або 6. вміння виступати китайською, але це не наш шлях. Ми хочемо, щоб ці якості проявлялись у кандидата максимально яскраво, тобто щоб наш кандидат був найбільш енергійним, сміливим і досвідченим у країні. Така людина всього одна, вона нам і треба. Отже нам потрібен механізм, який зможе виділити одну людину, а інших виключити з розгляду. Очевидно, вибори нам тут не допоможуть. Замість них потрібно дати об’яву наступного змісту (це може зробити ЦВК):
“Потрібен президент країни. Робочі години з 4 ранку до 11.59 вечора. Претендент має витримати три раунди з мером Києва (в перчатках). Після закінчення терміну - мученицька смерть за рідну країну. Якщо претендент знає конституцію (в останній редакції) лише на 95%, він буде фізично знищений. Якщо він набере менше 75% голосів при перевірці популярності за методом Гелапа, він також буде знищений. Крім цього претендент має звернутись з промовою на з’їзді виборців, які голосували виключно за Ю.В.Тимошенко з 1997 року і переконати їх у необхідності вільного продажу землі. У випадку провалу буде знищений. Приходити у спортклуб (вхід з двору) об 11.15. Перчатки надаються державою, кеди, майка і шорти - свої.”
Зауважте, що ця об’ява повністю позбавляє від бумажної роботи з анкетами, справками, деклараціями. Якщо все написати як слід, то прийде один претендент, який відразу може ставати до роботи. Але якщо не прийде ніхто? Це означає, що ми завищили вимоги, потрібно переписати об’яву. Замінимо 95 на 80, 75 на 65, і зробимо два раунди. І так далі, поки хтось таки не прийде.
Замість висновків
Загалом, механізм дизайн працює в ситуаціях, коли є гравці різних типів (умовно хороші і погані) і ми хочемо розробити систему правил, яка б розрізняла хороший і поганих і давала їм відповідні виграші. Добре налагоджений механізм має спонукати гравців говорити правду про свій тип, і, в ідеалі, давати хорошим перевагу. Це не означає, що прилітає фея і винагороджує хороших, просто (якщо говорити про економічні механізми), той хто діє кращим чином отримує більше грошей. Звичайно, одна з очевидних галузей застосування дизайну механізмів є державні політики і в наступній публікації ми спробуємо розібратись з механізмами фінансування суспільних проектів.
Рекомендації
-
Ivan Kozlov: Порошенко у польській Газеті Виборчій відповів на скандальну статтю Путіна. Переклад українською
Yulia Grypnyk, Armen Arakelyan, Наталія Куркова, Yana Bachynska, Hennadij Malanjuk та ще 20 користувачів





-
Ivan Kozlov: Хто замінить Андрія Шевченка? Маркевич, Ротань, Шовковський чи іноземець?
Stefko Rondel, Valentyna Poshtar, Alina Sorokina, Mazur Nazar




-
Александр Соколовский: Если не складывается, то может попробуем вычитать?
Іван Сірий, Николай Маркевич, Site Ua, Maksim Sidorenko, Borys Chornyi та ще 5 користувачів





-
Роман Доник: Вісім російських найманців побачили світло "руського міра" в кінці тунелю, протягом двох днів
Всеволод Поліщук, Yurii Tutko, Ігор Солод, Borys Chornyi, Vitalii Lypyn та ще 6 користувачів





-
Виктория Солодухина: Про українське кіно і стадо баранів.
Krikun Krikun, Михаил Очкас, Віктор Тальний



-
Serhiy Grigorovich: Великий день роздурачковуваня України ! Ч.1. Це саме те, що анонсувалося!
Vale Ntin, Серж Григоровский, Серг Тихонов, Krikun Krikun, Anna Maccagniani та ще 2 користувача





-
Yulia Grypnyk: ШОК! УКРАИНОЯЗЫЧНАЯ ЧЕЛЮСТЬ КНЯЗЯ ВОЛОДЫМЕРА! 10 фактов!
Stefko Rondel, Ruslana Pylypyshyn, Ivan Kozlov, Mark Telepko, Kateryna Yablonska та ще 39 користувачів





-
Павел Казарин: Кто может прийти после Путина
Gubenko Pavel, Yurii Tutko, Юрий Зеленков, Site Ua, Maksim Sidorenko та ще 20 користувачів





-
Роман Доник: "О новом главкоме замолвите слово" (18+)
Elena Shevchenko, Йозеф Швейк, Yurii Tutko, Alla Kondrik, Володимир Русанов та ще 34 користувача





-
Олексій Голобуцький: Факап з Чаусом: "Вова, ми стараємось"
Сергій Черняков, Іван Сірий, Зина Зинченко, Yurii Tutko, Alla Kondrik та ще 18 користувачів





Коментарі доступні тільки зареєстрованим користувачам
вхід / реєстрація